Active Noise Cancellation Using the Wiener Filter

Some situations arise where the signal of interest is corrupted by interference. A common example is air-to-ground communications. Consider the environment of a helicopter cockpit. Within the cockpit, audible noise is produced by the wind, the helicopter engine, and the pilot’s voice. In this case, the signal of interest is the pilot’s voice but this signal may be overwhelmed by the other noise sources. Simply creating a band-pass filter around the frequencies that lie within the human vocal range is insufficient to recover the signal of interest because the engine and wind interference may occupy the same frequencies. A better approach is to use an active noise cancellation system.

A noise canceling system requires two or more sensors, a primary sensor to measure the corrupted signal of interest and secondary sensors to measure the interference. It is important that the sensors measuring the interference be placed somewhere where it is possible to measure the interference but not the signal of interest. At this point, many assume that canceling the interference is simply a process of subtracting the interference measured at the secondary sensors from the signal containing both the desired signal and interference. In most cases, this approach fails or achieves little improvement. This is because the primary sensor rarely measures the interference with the exact same amplitude, phase, and distortion as the secondary sensors.

Going back to our helicopter example, the primary sensor may be a microphone located directly in front of the pilot’s mouth. The secondary sensors must be placed somewhere within the cockpit where they pick up the interference (the wind and engine noise) without picking up the pilot’s voice. Being spatially separated means that the sensors measure the noise from the wind and engine with different propagation delays, amplitudes, and may experience different distortions. However, because the unwanted noise measured at the primary and secondary sensors is generated by the same processes, the noise information between the two sensors is highly correlated. Thus it is possible to design a Wiener filter that filters the noise measured at the secondary sensors and produces an estimate of the noise measured at the primary sensor. This noise estimate is subtracted from the corrupted signal to produce an estimate of the signal of interest. Figure 1 is a block diagram that illustrates this concept.

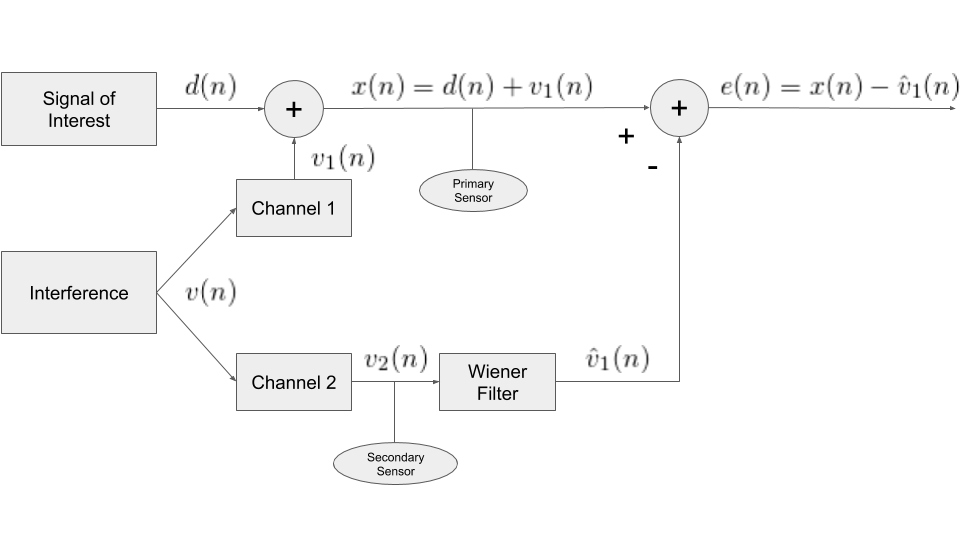
Post Notations

Before going on to the derivation, let’s define some notation so that we’re all on the same page. Let , and represent the expectation operator, the estimate of , and the autocorrelation function of respectively. The expectation operator returns the expected value or mean of a random variable. The estimate of  is found by filtering with our Wiener filter as follows

where is the number of filter coefficients.

The autocorrelation function for a wide sense stationary (WSS) signal is defined as

. 

The cross-correlation function for jointly WSS signals is defined as

Let the error be defined as the difference between the desired signal and the estimate of the desired signal

and the MSE be defined as 

.

Finally, let represent the complex conjugate operator. 

Deriving the Noise-Canceling Wiener Filter

The object of the Wiener filter is to minimize the mean squared error of the signal (check out this related Wiener filter post). For this derivation, it is assumed that the signal of interest and the interference are jointly wide sense stationary. A signal is wide sense stationary if the signal has constant mean, the autocorrelation depends only on the lag, and the variance is finite. As defined in the above diagram the error is the corrupted signal minus the estimate of the interference. With this definition, we derive the noise-cancelling Wiener filter.

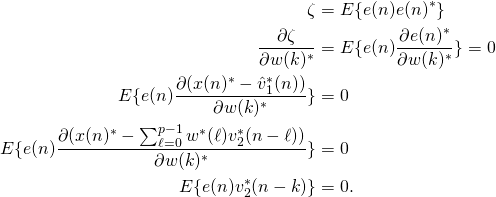
Now that the derivative is set to zero, we can solve for the filter coefficients that satisfy the equation.

However, if we let the desired signal, and the noise interference be uncorrelated (which in most cases is true) then and

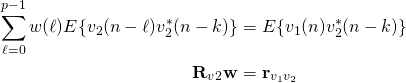
Unfortunately, we don’t have a sensor that measures exclusively, we have a sensor that measures which contains both the unwanted noise and the signal of interest. Basic algebra tells us that

Let’s see what happens when we substitute for for the cross correlation term.

If the signal of interest is uncorrelated with (this should be true in most practical cases) then the term on the right goes to zero and

This is much easier to work with because we have a sensor that records the signal . 

Noise Canceling Example

To better illustrate noise canceling using the Wiener filter, I have added three audio files. The first audio file is the observed signal . In this example, the unwanted noise interference, , is a simple tone that should be clearly audible. The second audio file is after the unwanted signal, , has been estimated from and removed, leaving the desired audio recording. The final file shows what would happen if the signal recorded from the secondary sensor, , was simply subtracted from . 

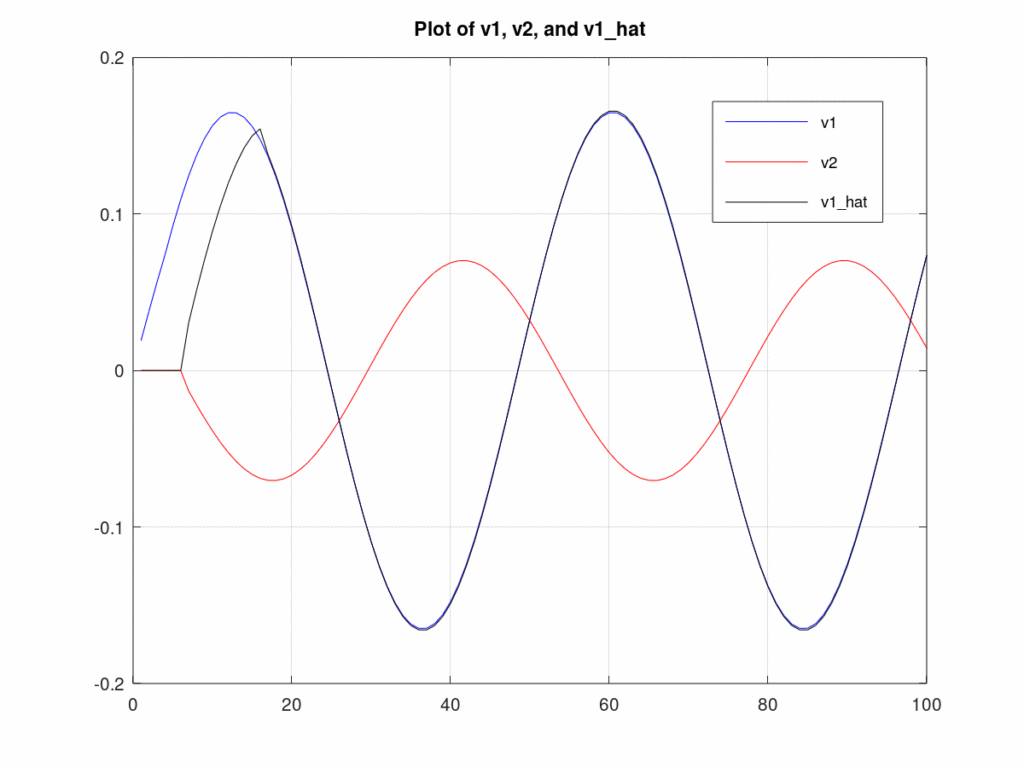
The pure tone was generated in simulation, thus we have access to it even though real applications would not. Plotting , , and can be helpful in understanding how the system works. Figure 2 plots these three signals. Notice that and are out of phase by nearly 180 degrees. It is now obvious why subtracting from had no effect, in fact subtracting from caused the tone to increase in power! Filtering with the Wiener filter produces , which now correctly matches in both phase and amplitude, allowing us to subtract it from to get our desired signal.